在问题开始之前，我们先做如下的假设。择偶者在年龄为a时开始进行选择，并确定在年龄为b以前一定完成选择。 而在a到b之间，不同的对象出现的概率是相等的。择偶者无法预测未来会出现什么样的人，但可以根据以前的情况 判断现在遇到的人是否合适。被拒绝的对象无法再次由择偶者回头选择，因为这个人可能已经结婚了或者被另外的人选择， 但是如果可以选择，可以看作是再次出现。
择偶者的要求是尽量选择的他们认为最优秀的对象。
择偶者在k年的拒绝之后，最后决定，如果后面一旦出现比前面k年遇到的对象优秀的人，就马上进行选择。 用Pk(best)表示这种选择策略能够选到最好对象的概率。而我们假设对于单个择偶者，最好的对象应该是 出现在开始择偶后的第X年（这一点，择偶者显然不清楚）。在X=i的条件下，由条件概率：
很容易得到，如果最好的对象出现在从选择开始的k年内，那么这个选择者便不可能再选到他认为最优秀的对象。这种 情况下Pk(best)是等于0的，即：
如果，i > k,择偶者必须在第i年进行选择，因为那个时候最好的对象才出现，我们才有机会计算Pk(best)。其他的情况 下Pk(best)=0。因此，k到i-1的选择中，必然没有出现比前k年的选择更优秀的对象。
继续推导，我们得到:
考虑上式(1)，我们得到函数：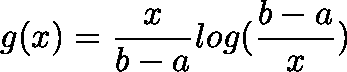
对上式求导，我们可以得到：
这样：
则择偶者在年龄等于a+(b-a)/e时有最大的概率选到最好的对象。 我们可以计算一下，如果一个人在16岁开始选择,并规定在36岁以前必须完成选择。我们可以计算出她做出决定的最佳年龄为16+(36-16)/(e)=23.4岁。
通常中国的男子一般会在17岁左右开始选择,在48岁左右结束,这样他们的最佳选择年龄为28.4岁。 而一般的中国女子还在16左右开始选择,平均在40岁左右结束。这样她们的最佳选择年龄为24.8岁。
以上只是一个概率上的分析，不过和实际的情况差别不大。是不是可以说明，人们进行选择的时候或多或少的服从了这样的概率假设和模型。
对于择偶者，这个分析也有很好的指导意义，即在有最大可能遇到最合适对象的年龄，择偶者应该好好特别留心，不要错过。
参考文献 ： Sheldon M.Ross ， Introduction to Probability Models, Eighth Edition，Academic Press，2006
（本分析其实是书中一个例子的翻版）
